
Tree, Binary Tree
09 Jan 2019 | DataStructure포스팅
concepts
트리는 그 모양이 뒤집어 놓은 나무와 같다고 해서 이런 이름이 붙었습니다. 예컨대 다음 그림과 같습니다.
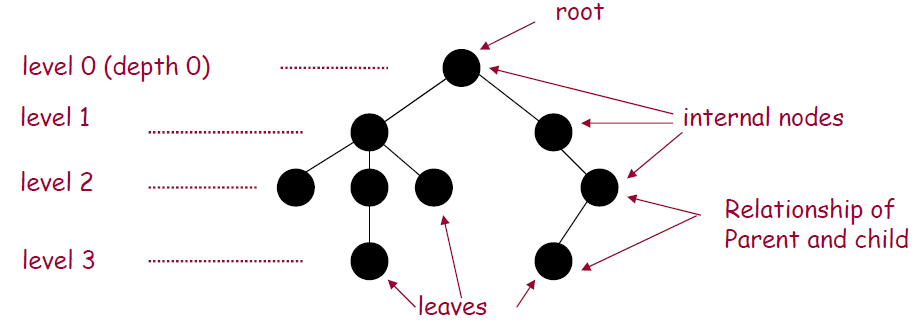 <내용>
<내용>
 <내용>
<내용>
 <내용>
<내용>
 <내용>
<내용>
Binary tree
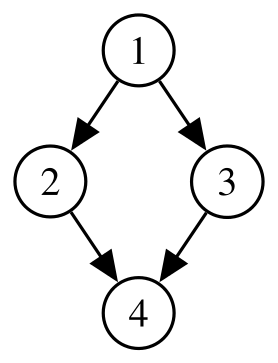
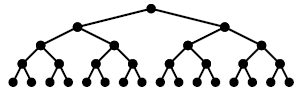
이진트리란 자식노드가 최대 두 개인 노드들로 구성된 트리입니다. 이진트리에는 정이진트리(full binary tree), 완전이진트리(complete binary tree), 균형이진트리(balanced binary tree) 등이 있습니다. 정이진트리는 다음 그림과 같습니다. 모든 레벨에서 노드들이 꽉 채워진(=잎새노드를 제외한 모든 노드가 자식노드를 2개 가짐) 이진트리입니다.
 <내용>
<내용>
 <내용>
<내용>
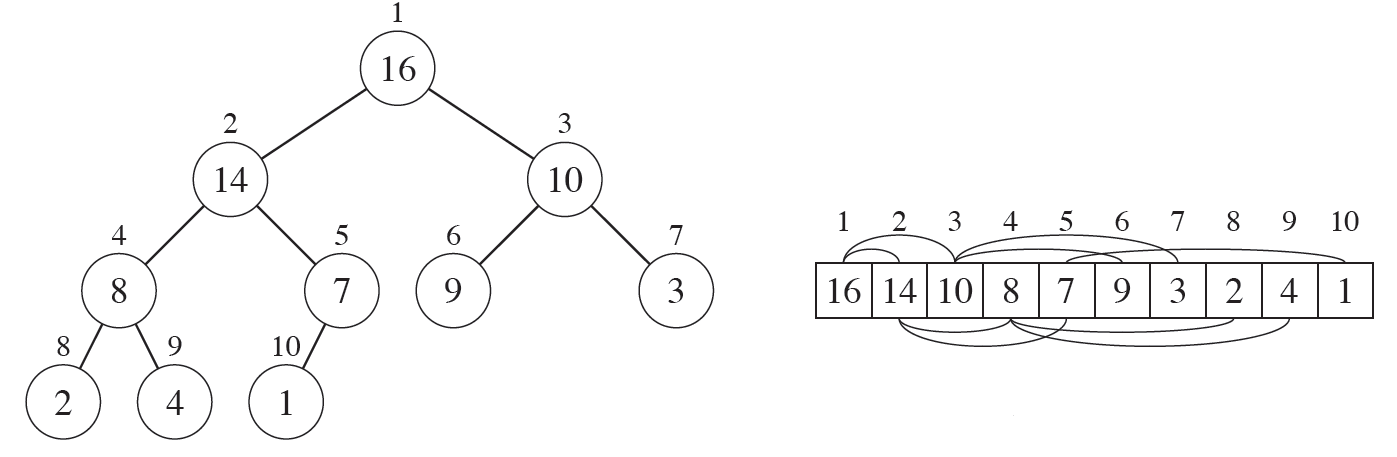 <내용>
<내용>
left_index = 2 * index + 1
right_index = 2 * index + 2
 <내용>
<내용>
tree traversal
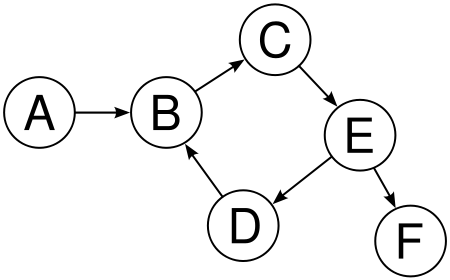
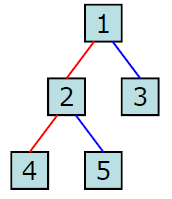
트리순회(tree traversal)란 트리의 각 노드를 체계적인 방법으로 방문하는 과정을 말합니다. 하나도 빠뜨리지 않고, 정확히 한번만 중복없이 방문해야 하는데요. 노드를 방문하는 순서에 따라 전위순회(preorder), 중위순회(inorder), 후위순회(postorder) 세 가지로 나뉩니다. 아래 트리를 예시로 각 방법 간 차이를 비교해 보겠습니다.
 <내용>
<내용>
preorder
루트 노드에서 시작해서 노드-왼쪽 서브트리-오른쪽 서브트리 순으로 순회하는 방식입니다. 깊이우선순회(depth-first traversal)라고도 합니다. 위 예시 트리에 전위순회 방식을 적용하면 다음과 같습니다. $1, 2, 4, 5, 3$inorder
루트 노드에서 시작해서 왼쪽 서브트리-노드-오른쪽 서브트리 순으로 순회하는 방식입니다. 대칭순회(symmetric traversal)라고도 합니다. 위 예시 트리를 중위순회 방식을 적용하면 다음과 같습니다. $4, 2, 5, 1, 3$postorder
루트 노드에서 시작해서 왼쪽 서브트리-오른쪽 서브트리-노드 순으로 순회하는 방식입니다. 위 예시 트리를 후위순회 방식을 적용하면 다음과 같습니다. $4, 5, 2, 3, 1$예시 : 사칙연산
예컨대 다음과 같은 식을 계산해야 한다고 칩시다. $(A+B)×(C+D)+2$ 이를 후위표기법으로 바꿔서 다시 쓰면 다음과 같습니다. 후위표기법은 이곳을 참고하시면 좋을 것 같습니다. $AB+CD+×2+$ 컴퓨터가 사칙연산을 수행할 때 이진트리를 쓰면 편리합니다. 아래 그림을 볼까요? <그림 10.> 위 이진트리를 후위순회 방식으로 읽어 보겠습니다. 이는 정확히 후위표기법과 일치합니다. $A, B, +, C, D, +, ×, 2, +$ 위 이진트리를 전위순회 방식으로 읽어 보겠습니다. 다음과 같습니다. $+, ×, +, A, B, +, C, D, 2$ 이는 함수명(인자) 형태의 함수호출과 동일합니다. 예컨대 + 기호를 add 함수, ×를 multiply 함수라고 생각해 보죠. 그러면 위와 같은 시퀀스는 다음과 같이 수행됩니다. $add(multiply(add(A, B), add(C, D)), 2)$가져온곳: URL
