ysw's blog

Queue

07 Jan 2019 | DataStructure

포스팅

concept

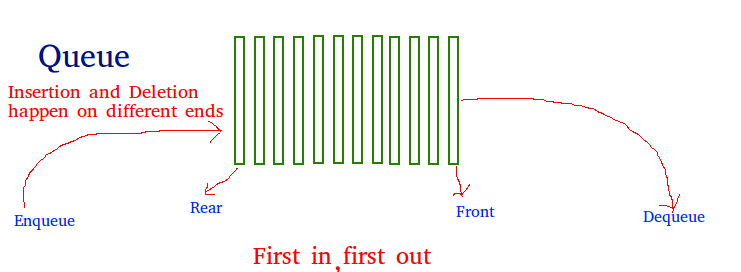
큐란 목록 한쪽 끝에서만 자료를 넣거나 뺄 수 있는 자료구조의 일종입니다. 먼저 집어넣은 데이터가 먼저 나오는 FIFO(First In First Out) 구조로 저장하는 형식을 가리킵니다. 사람들이 표를 사거나 순서를 기다리려고 일렬로 늘어선 줄(queue)을 연상하면 이해가 쉽습니다. 다시 말해 먼저 줄을 선 사람(데이터)이 먼저 나갈 수 있다는 것이지요. 구조를 보면 다음 그림과 같습니다.

<내용>

큐에 새로운 데이터가 들어오면 큐의 끝 위치(tail)에 저장이 됩니다. 반대로 삭제할 때는 첫번째 위치(head)의 요소가 지워지게 됩니다. 전자를 $enqueue$, 후자를 $dequeue$라고 합니다.

operation

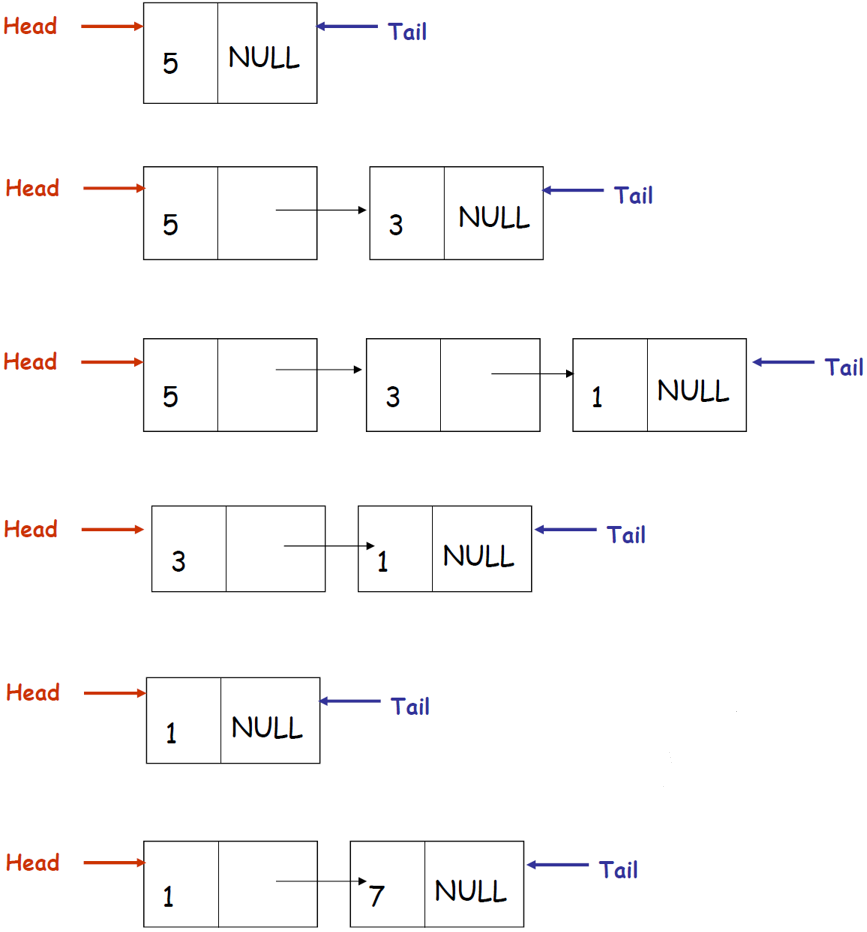
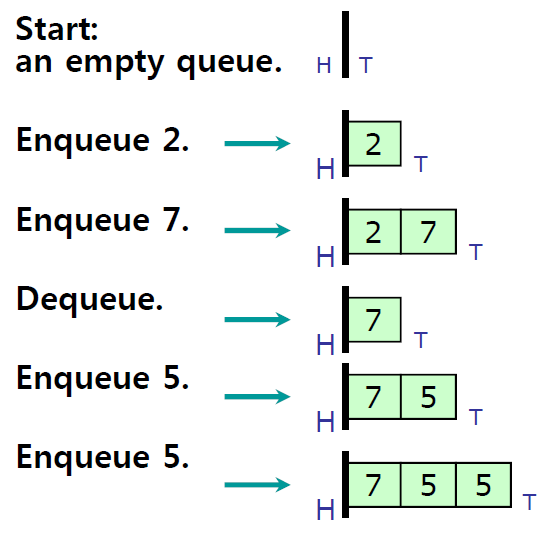
큐의 핵심 연산은 $enqueue$와 $dequeue$입니다. 연결리스트(linked list) 형태로 큐를 구현했을 때 예시는 다음과 같습니다.
$enqueue5 -> enqueue3 -> enqueue1 -> dequeue -> dequeue -> enqueue7$

<내용>

연결리스트로 큐를 구현했을 때 $enqueue$와 $dequeue$의 계산복잡성은 모두 $O(1)$입니다. 추가, 삭제 연산이 각각 큐의 시작(head)과 끝(tail)에서만 일어나기 때문입니다.

큐를 array로 구현할 수도 있습니다. 다음과 같습니다.

<내용>

array로 큐를 구현했을 때 $enqueue$의 계산복잡성은 $O(1)$입니다. 추가 연산이 큐의 끝(tail)에서만 일어나기 때문입니다. 그러나 $dequeue$의 계산복잡성은 $O(n)$이 됩니다. 큐의 시작(head) 요소를 지우게 되면 두번째 요소부터 끝에 이르는 모든 요소들의 위치를 왼쪽으로 한 칸씩 옮겨주어야 하기 때문입니다.

Circular Array로 큐를 구현하면 이러한 문제를 해결할 수 있습니다. 그 개념도는 다음과 같습니다. Circular Array를 쓰면 enqueue, dequeue가 각각 큐의 시작(head)과 끝(tail)에서만 일어나게 돼 둘 모두 계산복잡성이 $O(1)$이 됩니다.

<내용>

파이썬 구현 파이썬에서 Circular Array로 구현한 큐는 다음과 같습니다.

class CircularQueue():

    # Constructor
    def __init__(self):
        self.queue = list()
        self.head = 0
        self.tail = 0
        self.maxSize = 8

    # Adding elements to the queue
    def enqueue(self,data):
        if self.size() == self.maxSize-1:
            return ("Queue Full!")
        self.queue.append(data)
        self.tail = (self.tail + 1) % self.maxSize
        return True

    # Removing elements from the queue
    def dequeue(self):
        if self.size()==0:
            return ("Queue Empty!") 
        data = self.queue[self.head]
        self.head = (self.head + 1) % self.maxSize
        return data

    # Calculating the size of the queue
    def size(self):
        if self.tail>=self.head:
            return (self.tail-self.head)
        return (self.maxSize - (self.head-self.tail))

가져온곳: URL